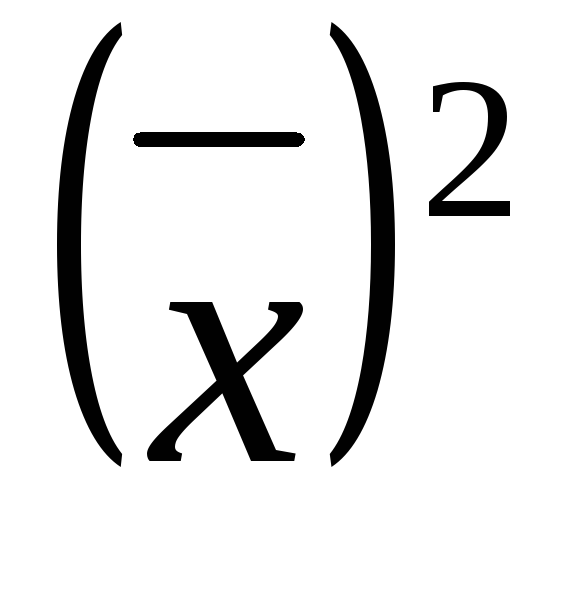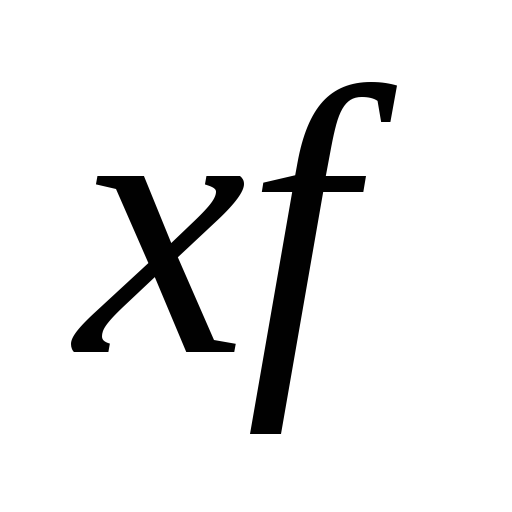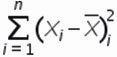Дисперсия
– это средняя арифметическая квадратов
отклонений каждого значения признака
от общей средней. Дисперсия обычно
называется средним квадратом отклонений.
В зависимости от исходных данных
дисперсия может вычисляться по средней
арифметической простой или взвешенной:
Для
не сгруппированных данных σ 2
=,
Для
вариационного ряда σ 2
=
.
Среднее
квадратическое
отклонение
представляет собой корень квадратный
из дисперсии:
Для
не сгруппированных данных σ =
,Для
вариационного ряда σ =
.
Среднее
квадратическое отклонение – это
обобщающая характеристика абсолютных
размеров вариации признака в совокупности.
Выражается оно в тех же единицах
измерения, что и признак (в метрах,
тоннах, процентах, гектарах и т.д.).
Вычислению
среднего квадратического отклонения
предшествует расчёт дисперсии.
Определение
дисперсии и среднего квадратического
отклонения по индивидуальным значениям
Порядок
расчета:
по
значениям признака исчисляется средняя
арифметическая простая
;
Задание
3.
По примеру
двух бригад (задание 1) определите
дисперсию и среднее квалратическое
отклонение производительности труда.
Методика
решения:
Определение
дисперсии и среднего квадратического
отклонения в дискретных и интервальных
рядах распределения
Порядок
расчета:
Задание
4.
Рассчитайте
дисперсию и среднее квадратическое
отклонение по данным типовой задачи.
Сделайте вывод.
|
Произведено |
Число |
||||
Методика
решения:
Если
исходные данные представлены в виде
интервального ряда распределения, то
сначала надо определить дискретное
значение признака, а далее применить
тот же метод, что изложен выше.
Задание
5.
Рассчитайте
дисперсию и среднее квадратическое
отклонение для интервального ряда по
данным распределения посевной площади
хозяйства по урожайности пшеницы:
|
Урожайность |
Посевная |
|||||
Методика
решения:
Расчет
дисперсии упрощенным способом.
Применение
приведенной формулы расчета дисперсии
не всегда удобно, хотя она хорошо отражает
суть показателя. Поэтому необходимо
знать другую формулу упрощенного способа
расчета, вытекающую из приведенной
выше:
,где
–
средняя величина квадратов вариантов;
–
квадрат средней арифметической.
Порядок
расчета (если данные несгруппированы):
Задание
6.
Имеются
данные о производительности труда
рабочих.Вычислить дисперсию упрощенным
способом.
|
№ рабочего |
Произведена |
|
Методика
решения:
Порядок
расчета (если данные сгруппированы):
Задание
7.
Имеются
данные о распределении сельскохозяйственных
предприятий по наличию основных фондов.
Вычислить дисперсию упрощенным способом.
|
Группы |
Число |
||||
Методика
решения.
Дисперсия
– это средняя арифметическая квадратов отклонений каждого значения признака от общей средней. В зависимости от исходных данных дисперсия может быть невзвешенной (простой) или взвешенной.
Дисперсия рассчитывается по следующим формулам:
· для несгруппированных данных
· для сгруппированных данных
Порядок расчета дисперсии взвешенную:
1. определяют среднюю арифметическую взвешенную
2. определяются отклонения вариант от средней
3. возводят в квадрат отклонение каждой варианты от средней
4. умножают квадраты отклонений на веса (частоты)
5. суммируют полученные произведения
6. полученную сумму делят на сумму весов
Формула для определения дисперсии может быть преобразована в следующую формулу:
Простая
Порядок расчета дисперсии простой:
1. определяют среднюю арифметическую
2. возводят в квадрат среднюю арифметическую
3. возводят в квадрат каждую варианту ряда
4. находим сумму квадратов вариант
5. делят сумму квадратов вариант на их число, т.е. определяют средний квадрат
6. определяют разность между средним квадратом признака и квадратом средней
Также формула для определения дисперсии взвешенной может быть преобразована в следующую формулу:
т.е. дисперсия равна разности средней из квадратов значений признака и квадрата средней арифметической. При пользовании преобразованной формулой исключается дополнительная процедура по расчету отклонений индивидуальных значений признака от х и исключается ошибка в расчете, связанная с округлением отклонений
Дисперсия обладает рядом свойств, некоторые из них позволяют упростить ее вычисления:
1) дисперсия постоянной величины равна нулю;
2) если все варианты значений признака уменьшить на одно и то же число, то дисперсия не уменьшится;
3) если все варианты значений признака уменьшить в одно и то же число раз ( раз), то дисперсия уменьшится в раз
Среднее квадратичное отклонение S
– представляет собой корень квадратный из дисперсии:
· для несгруппированных данных:
· для вариационного ряда:
Размах вариации, среднее линейное и среднее квадратичное отклонение являются величинами именованными. Они имеют те же единицы измерения, что и индивидуальные значения признака.
Дисперсия и среднее квадратическое отклонение наиболее широко применяемые показатели вариации. Объясняется это тем, что они входят в большинство теорем теории вероятности, служащей фундаментом математической статистики. Кроме того, дисперсия может быть разложена на составные элементы, позволяющие оценить влияние различных факторов, обусловливающих вариацию признака.
Расчет показателей вариации для банков, сгруппированных по размеру прибыли, показан в таблице.
| Размер прибыли, млн. руб. | Число банков | расчетные показатели | ||||
| 3,7 – 4,6 (-) | 4,15 | 8,30 | -1,935 | 3,870 | 7,489 | |
| 4,6 – 5,5 | 5,05 | 20,20 | – 1,035 | 4,140 | 4,285 | |
| 5,5 – 6,4 | 5,95 | 35,70 | – 0,135 | 0,810 | 0,109 | |
| 6,4 – 7,3 | 6,85 | 34,25 | +0,765 | 3,825 | 2,926 | |
| 7,3 – 8,2 | 7,75 | 23,25 | +1,665 | 4,995 | 8,317 | |
| Итого: | 121,70 | 17,640 | 23,126 |
Среднее линейное и среднее квадратичное отклонение показывают на сколько в среднем колеблется величина признака у единиц и исследуемой совокупности. Так, в данном случае средняя величина колеблености размера прибыли составляет: по среднему линейному отклонению 0,882 млн. руб.; по среднему квадратическому отклонению – 1,075 млн. руб. Среднее квадратическое отклонение всегда больше среднего линейного отклонения. Если распределение признака, близко к нормальному, то между S и d существует взаимосвязь: S=1,25d, или d=0,8S. Среднее квадратическое отклонение показывает как расположена основная масса единиц совокупности относительно средней арифметической. Независимо от формы распределения 75 значений признака попадают в интервал х 2S, а по крайне мере 89 всех значений попадают интервал х 3S (теорема П.Л.Чебышева).
При статистической проверке гипотез, при измерении линейной взаимосвязи между случайными величинами.
Среднеквадратическое отклонение:
Стандартное отклонение
(оценка среднеквадратического отклонения случайной величины Пол, стены вокруг нас и потолок,x
относительно её математического ожидания на основе несмещённой оценки её дисперсии):
где – дисперсия ; – Пол, стены вокруг нас и потолок,i
-й элемент выборки; – объём выборки; – среднее арифметическое выборки:
Следует отметить, что обе оценки являются смещёнными. В общем случае несмещённую оценку построить невозможно. Однако оценка на основе оценки несмещённой дисперсии является состоятельной .
Правило трёх сигм
Правило трёх сигм
() – практически все значения нормально распределённой случайной величины лежат в интервале . Более строго – не менее чем с 99,7 % достоверностью значение нормально распределенной случайной величины лежит в указанном интервале (при условии, что величина истинная, а не полученная в результате обработки выборки).
Если же истинная величина неизвестна, то следует пользоваться не , а Пол, стены вокруг нас и потолок,s
. Таким образом, правило трёх сигм преобразуется в правило трёх Пол, стены вокруг нас и потолок,s
.
Интерпретация величины среднеквадратического отклонения
Большое значение среднеквадратического отклонения показывает большой разброс значений в представленном множестве со средней величиной множества; маленькое значение, соответственно, показывает, что значения в множестве сгруппированы вокруг среднего значения.
Например, у нас есть три числовых множества: {0, 0, 14, 14}, {0, 6, 8, 14} и {6, 6, 8, 8}. У всех трёх множеств средние значения равны 7, а среднеквадратические отклонения, соответственно, равны 7, 5 и 1. У последнего множества среднеквадратическое отклонение маленькое, так как значения в множестве сгруппированы вокруг среднего значения; у первого множества самое большое значение среднеквадратического отклонения – значения внутри множества сильно расходятся со средним значением.
В общем смысле среднеквадратическое отклонение можно считать мерой неопределенности. К примеру, в физике среднеквадратическое отклонение используется для определения погрешности серии последовательных измерений какой-либо величины. Это значение очень важно для определения правдоподобности изучаемого явления в сравнении с предсказанным теорией значением: если среднее значение измерений сильно отличается от предсказанных теорией значений (большое значение среднеквадратического отклонения), то полученные значения или метод их получения следует перепроверить.
Практическое применение
На практике среднеквадратическое отклонение позволяет определить, насколько значения в множестве могут отличаться от среднего значения.
Климат
Предположим, существуют два города с одинаковой средней максимальной дневной температурой, но один расположен на побережье, а другой внутри континента. Известно, что в городах, расположенных на побережье, множество различных максимальных дневных температур меньше, чем у городов, расположенных внутри континента. Поэтому среднеквадратическое отклонение максимальных дневных температур у прибрежного города будет меньше, чем у второго города, несмотря на то, что среднее значение этой величины у них одинаковое, что на практике означает, что вероятность того, что максимальная температура воздуха каждого конкретного дня в году будет сильнее отличаться от среднего значения, выше у города, расположенного внутри континента.
Спорт
Предположим, что есть несколько футбольных команд, которые оцениваются по некоторому набору параметров, например, количеству забитых и пропущенных голов, голевых моментов и т. п. Наиболее вероятно, что лучшая в этой группе команда будет иметь лучшие значения по большему количеству параметров. Чем меньше у команды среднеквадратическое отклонение по каждому из представленных параметров, тем предсказуемее является результат команды, такие команды являются сбалансированными. С другой стороны, у команды с большим значением среднеквадратического отклонения сложно предсказать результат, что в свою очередь объясняется дисбалансом, например, сильной защитой, но слабым нападением.
Использование среднеквадратического отклонения параметров команды позволяет в той или иной мере предсказать результат матча двух команд, оценивая сильные и слабые стороны команд, а значит, и выбираемых способов борьбы.
Технический анализ
См. также
Литература
* Боровиков, В.
STATISTICA. Искусство анализа данных на компьютере: Для профессионалов / В. Боровиков. – СПб.
: Питер, 2003. – 688 с. – ISBN 5-272-00078-1
.
| Статистические показатели | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Описательная статистика |
|
||||||||||
| Статистический вывод и проверка гипотез |
|
||||||||||
При статистической проверке гипотез, при измерении линейной взаимосвязи между случайными величинами.
Среднеквадратическое отклонение:
Стандартное отклонение
(оценка среднеквадратического отклонения случайной величины Пол, стены вокруг нас и потолок,x
относительно её математического ожидания на основе несмещённой оценки её дисперсии):
где – дисперсия ; – Пол, стены вокруг нас и потолок,i
-й элемент выборки; – объём выборки; – среднее арифметическое выборки:
Следует отметить, что обе оценки являются смещёнными. В общем случае несмещённую оценку построить невозможно. Однако оценка на основе оценки несмещённой дисперсии является состоятельной .
Правило трёх сигм
Правило трёх сигм
() – практически все значения нормально распределённой случайной величины лежат в интервале . Более строго – не менее чем с 99,7 % достоверностью значение нормально распределенной случайной величины лежит в указанном интервале (при условии, что величина истинная, а не полученная в результате обработки выборки).
Если же истинная величина неизвестна, то следует пользоваться не , а Пол, стены вокруг нас и потолок,s
. Таким образом, правило трёх сигм преобразуется в правило трёх Пол, стены вокруг нас и потолок,s
.
Интерпретация величины среднеквадратического отклонения
Большое значение среднеквадратического отклонения показывает большой разброс значений в представленном множестве со средней величиной множества; маленькое значение, соответственно, показывает, что значения в множестве сгруппированы вокруг среднего значения.
Например, у нас есть три числовых множества: {0, 0, 14, 14}, {0, 6, 8, 14} и {6, 6, 8, 8}. У всех трёх множеств средние значения равны 7, а среднеквадратические отклонения, соответственно, равны 7, 5 и 1. У последнего множества среднеквадратическое отклонение маленькое, так как значения в множестве сгруппированы вокруг среднего значения; у первого множества самое большое значение среднеквадратического отклонения – значения внутри множества сильно расходятся со средним значением.
В общем смысле среднеквадратическое отклонение можно считать мерой неопределенности. К примеру, в физике среднеквадратическое отклонение используется для определения погрешности серии последовательных измерений какой-либо величины. Это значение очень важно для определения правдоподобности изучаемого явления в сравнении с предсказанным теорией значением: если среднее значение измерений сильно отличается от предсказанных теорией значений (большое значение среднеквадратического отклонения), то полученные значения или метод их получения следует перепроверить.
Практическое применение
На практике среднеквадратическое отклонение позволяет определить, насколько значения в множестве могут отличаться от среднего значения.
Климат
Предположим, существуют два города с одинаковой средней максимальной дневной температурой, но один расположен на побережье, а другой внутри континента. Известно, что в городах, расположенных на побережье, множество различных максимальных дневных температур меньше, чем у городов, расположенных внутри континента. Поэтому среднеквадратическое отклонение максимальных дневных температур у прибрежного города будет меньше, чем у второго города, несмотря на то, что среднее значение этой величины у них одинаковое, что на практике означает, что вероятность того, что максимальная температура воздуха каждого конкретного дня в году будет сильнее отличаться от среднего значения, выше у города, расположенного внутри континента.
Спорт
Предположим, что есть несколько футбольных команд, которые оцениваются по некоторому набору параметров, например, количеству забитых и пропущенных голов, голевых моментов и т. п. Наиболее вероятно, что лучшая в этой группе команда будет иметь лучшие значения по большему количеству параметров. Чем меньше у команды среднеквадратическое отклонение по каждому из представленных параметров, тем предсказуемее является результат команды, такие команды являются сбалансированными. С другой стороны, у команды с большим значением среднеквадратического отклонения сложно предсказать результат, что в свою очередь объясняется дисбалансом, например, сильной защитой, но слабым нападением.
Использование среднеквадратического отклонения параметров команды позволяет в той или иной мере предсказать результат матча двух команд, оценивая сильные и слабые стороны команд, а значит, и выбираемых способов борьбы.
Технический анализ
См. также
Литература
* Боровиков, В.
STATISTICA. Искусство анализа данных на компьютере: Для профессионалов / В. Боровиков. – СПб.
: Питер, 2003. – 688 с. – ISBN 5-272-00078-1
.
| Статистические показатели | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Описательная статистика |
|
||||||||||
| Статистический вывод и проверка гипотез |
|
||||||||||
Цель данной статьи показать
, как математические формулы, с которыми вы можете столкнуться в книгах и статьях, разложить на элементарные функции в Excel.
В данной статье мы разберем формулы среднеквадратического отклонения и дисперсии и рассчитаем их в Excel
.
Перед тем как переходить к расчету среднеквадратического отклонения и разбирать формулу, желательно разобраться в элементарных статистических показателях и обозначениях.
Рассматривая формулы моделей прогнозирования, мы встретимся со следующими показателями:
Например, у нас есть временной ряд – продажи по неделям в шт.
Для этого временного ряда i=1, n=10
,
,
Рассмотрим формулу среднего значения:
Для нашего временного ряда определим среднее значение
Также для выявления тенденций помимо среднего значения представляет интерес и то, насколько наблюдения разбросаны относительно среднего. Среднеквадратическое отклонение показывает меру отклонения наблюдений относительно среднего.
Формула расчета среднеквадратического отклонение для выборки следующая:
Разложим формулу на составные части и рассчитаем среднеквадратическое отклонение в Excel на примере нашего временного ряда.
1. Рассчитаем среднее значение для этого воспользуемся формулой Excel =СРЗНАЧ(B11:K11)
2. Определим отклонение каждого значения ряда относительно среднего
для первой недели = 6-10=-4
для второй недели = 10-10=0
для третей = 7-1=-3 и т.д.
3. Для каждого значения ряда определим квадрат разницы отклонения значений ряда относительно среднего
для первой недели = (-4)^2=16
для второй недели = 0^2=0
для третей = (-3)^2=9 и т.д.
4. Рассчитаем сумму квадратов отклонений значений относительно среднего
с помощью формулы =СУММ(ссылка на диапазон (ссылка на диапазон с )